#2533. 中位数----cx202004
中位数----cx202004
Background
数学中,我们经常这么来定义中位数:有 个数,从小到大排序以后,排名中间的数就是中位数,当 是奇数的时候,中位数只有 个,当 是偶数的时候,中间两个数都是中位数。注意,我们这里用到都是 个数的中位数。比如,有 个数 ,那么中位数就是 ,如果有 个数 ,那么中位数就是 。 我们有一个神奇的三角形,这个三角形的第 行只有 个数,第 行有 个数,第 行有 个数。下图就是一个简单的例子:
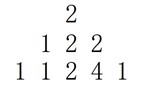
这里的第 行(也就是最后一行)是提前给定的,剩余的数都是按照规则产生的。第 行第 列的数是第 行第 列和第 行第 列和第 行第 这 个数的中位数。这里第 行第 列的 是 的中位数,第 行第 列的 是 的中位数,第 行第 列的数是 的中位数,第 行第 列的数是 的中位数。 现在我们的问题是告诉你总共有 行,以及最后一行的 个数,请你算出第行第 列上的那个数是多少。
Input
输入的第一行是一个正整数 ,表示这个三角形的层数。
接下来一行有 个整数 ,表示最后一行上的整数,中间用一个空格隔开。
Output
输出第 行第 列上的数,也就是第 行唯一的那个数
Samples
3
2 3 2 5 1
2
5
4 3 3 6 7 4 6 3 7
6
10
5 8 1 1 7 6 6 5 8 6 2 9 9 5 9 4 2 9 3
6
Limitation
【数据规模】
对于所有的数据 。